Lecture 16: Dijkstra’s Algorithm
COSC 311 Algorithms, Fall 2022
$ \def\compare{ {\mathrm{compare}} } \def\swap{ {\mathrm{swap}} } \def\sort{ {\mathrm{sort}} } \def\insert{ {\mathrm{insert}} } \def\true{ {\mathrm{true}} } \def\false{ {\mathrm{false}} } \def\BubbleSort{ {\mathrm{BubbleSort}} } \def\SelectionSort{ {\mathrm{SelectionSort}} } \def\Merge{ {\mathrm{Merge}} } \def\MergeSort{ {\mathrm{MergeSort}} } \def\QuickSort{ {\mathrm{QuickSort}} } \def\Split{ {\mathrm{Split}} } \def\Multiply{ {\mathrm{Multiply}} } \def\Add{ {\mathrm{Add}} } \def\cur{ {\mathrm{cur}} } \def\gets{ {\leftarrow} } $
Overview
- Recap of DFS
- Weighted Graphs
- Weighted Shortest Paths
- Dijkstra’s Algorithm
Last Time
Unweighted Single-Source Shortest Paths:
- Given graph $G = (V, E)$ and starting vertex $u$
- Find for every vertex $v$, the distance $d(u, v)$
- $d(u, v) =$ length of shortest path from $u$ to $v$
- shortest $= $ fewest hops
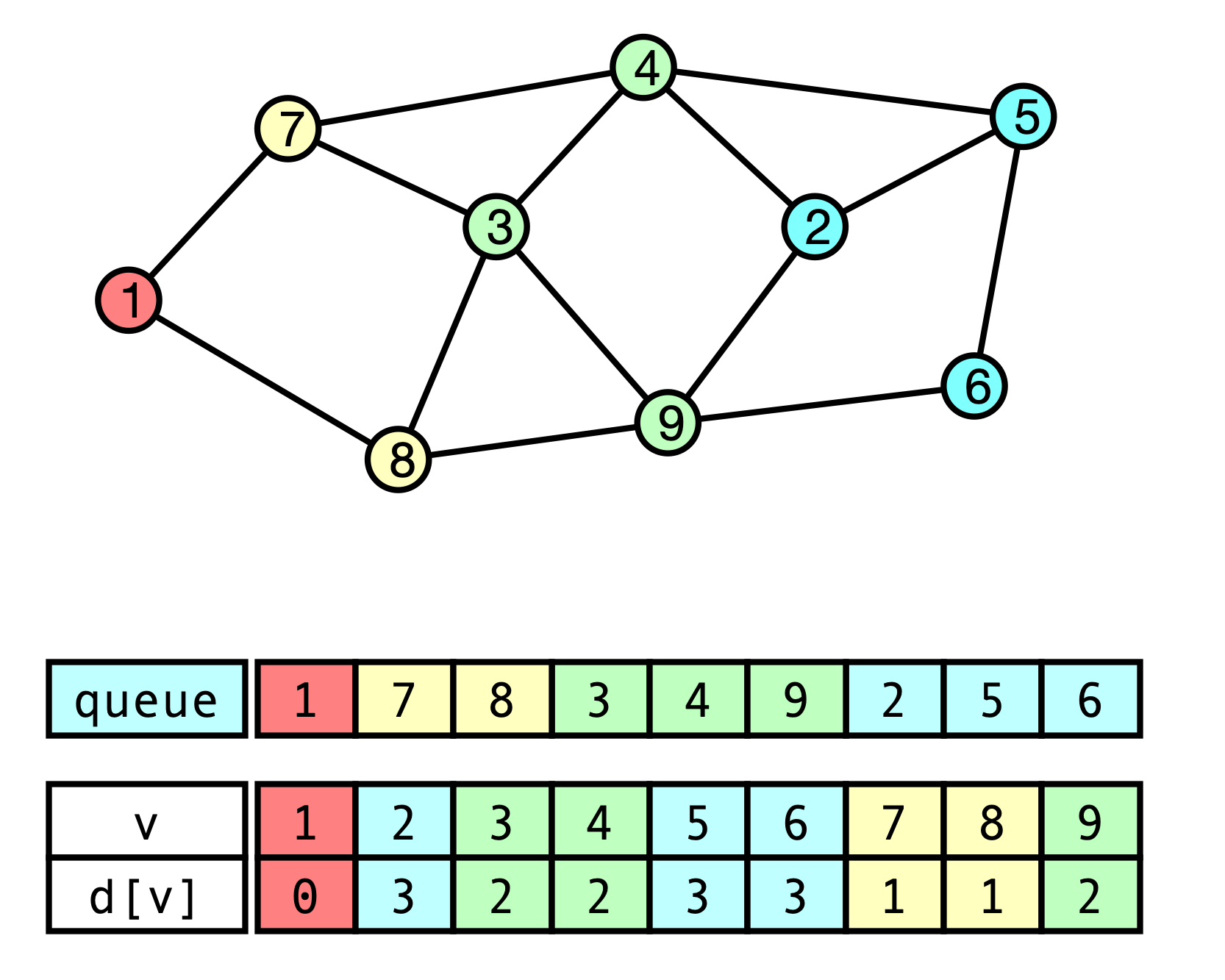
Solution: Breadth-first Search (BFS)
- Process vertices in increasing order of distance from $u$
BFS Pseudocode
BFS(V, E, u):
intialize d[v] <- -1 for all v
d[u] <- 0
queue.add(u)
while queue is not empty do
v <- queue.remove()
for each neighbor w of v do
if d[w] = -1 then
d[w] <- d[v] + 1
queue.add(w)
return d
Correctness. Follows from interaction with queue: vertices added in order of increasing distance from $u$
- $\implies$ distance is correct when vertex added
BFS Phases
BFS Running Time?
BFS(V, E, u):
intialize d[v] <- -1 for all v
d[u] <- 0
queue.add(u)
while queue is not empty do
v <- queue.remove()
for each neighbor w of v do
if d[w] = -1 then
d[w] <- d[v] + 1
queue.add(w)
return d
More General Problem
Definition. A weighted graph is a graph $G(V, E)$ where each edge $e \in E$ is additionally assigned a (real valued) weight $w(e)$.
- for now, assume $w(e) \geq 0$
Examples.
- weights = distances (not just number of hops)
- weights = cost of connection
- weights = latency of connection
- …
Distance in Weighted Graphs
-
$G = (V, E)$ a graph, $w$ weights
-
$P = v_0 e_1 v_1 e_2 v_2 \cdots e_k v_k$ a path
-
The (weighted) length of $P$ is
\[w(P) = w(e_1) + w(e_2) + \cdots + w(e_k)\]
Example
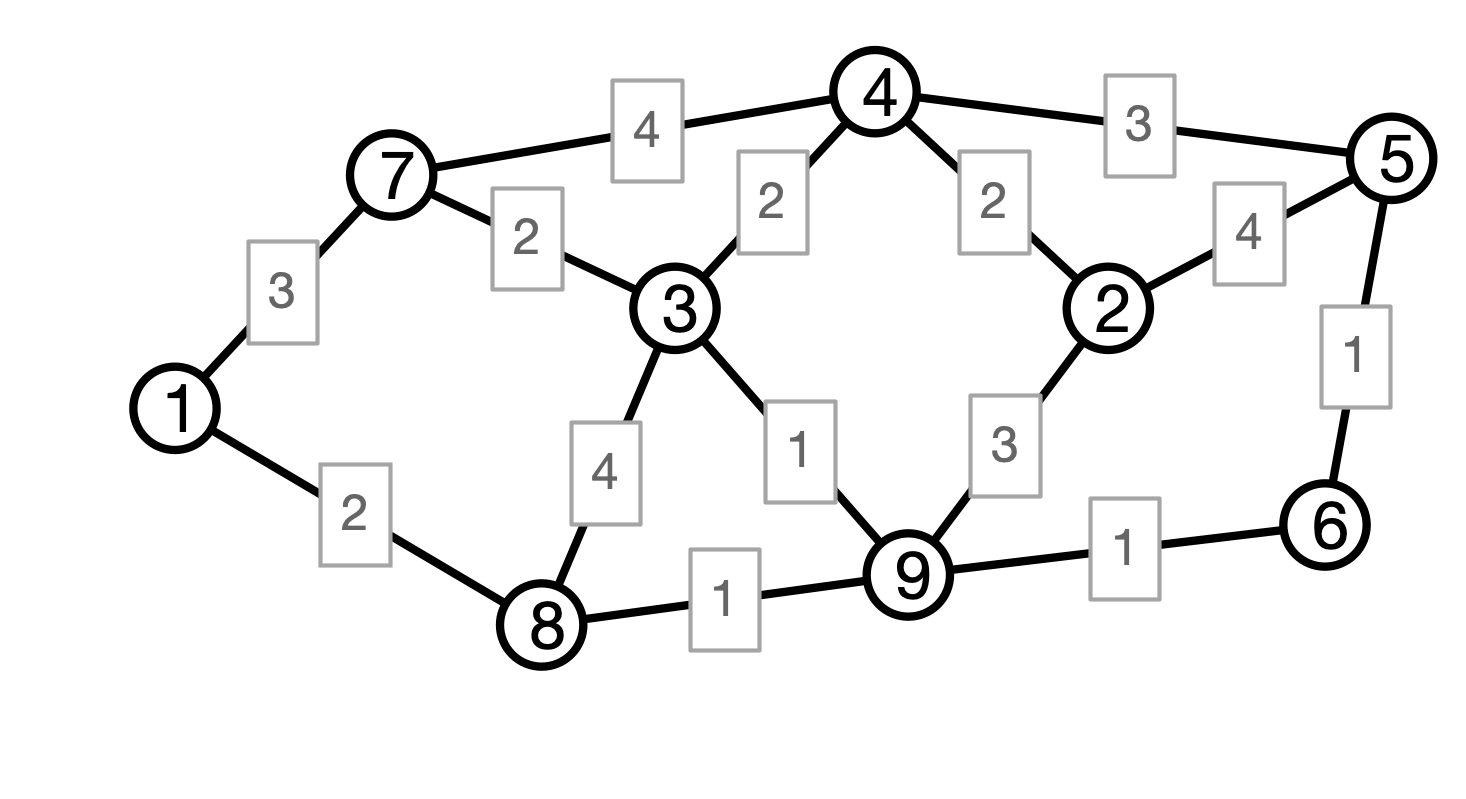
Weighted Shortest Paths
Given weights $w$, define $d_w(u, v)$ to be minimum (weighted) length of any path $P$ from $u$ to $v$.
Example

What is $d_w(1, 3)$? What about $d_w(1, 5)$?
Weighted SSSP
Input.
- a weighted Graph $G = (V, E)$, edge weights $w$
- an initial vertex $u \in V$
- each vertex $v \in V$ has associated adjacency list
- list of $v$’s neighbors
- includes weight of edge from $v$ to each neighbor
Output.
-
A map $d: V \to \mathbf{R}$ such that $d[v] = d_w(u, v)$ is the graph distance from $u$ to $v$
- $d[v] = \infty$ indicates no path from $u$ to $v$
Weighted SSSP
Does BFS compute weighted distances from $u$?
- must update procedure
- when processing edge $(v, x)$, should update $d[x] \gets d[v] + w(v, x)$ rather than setting $d[x] \gets d[v] + 1$
Does this work?
Weighted BFS Example
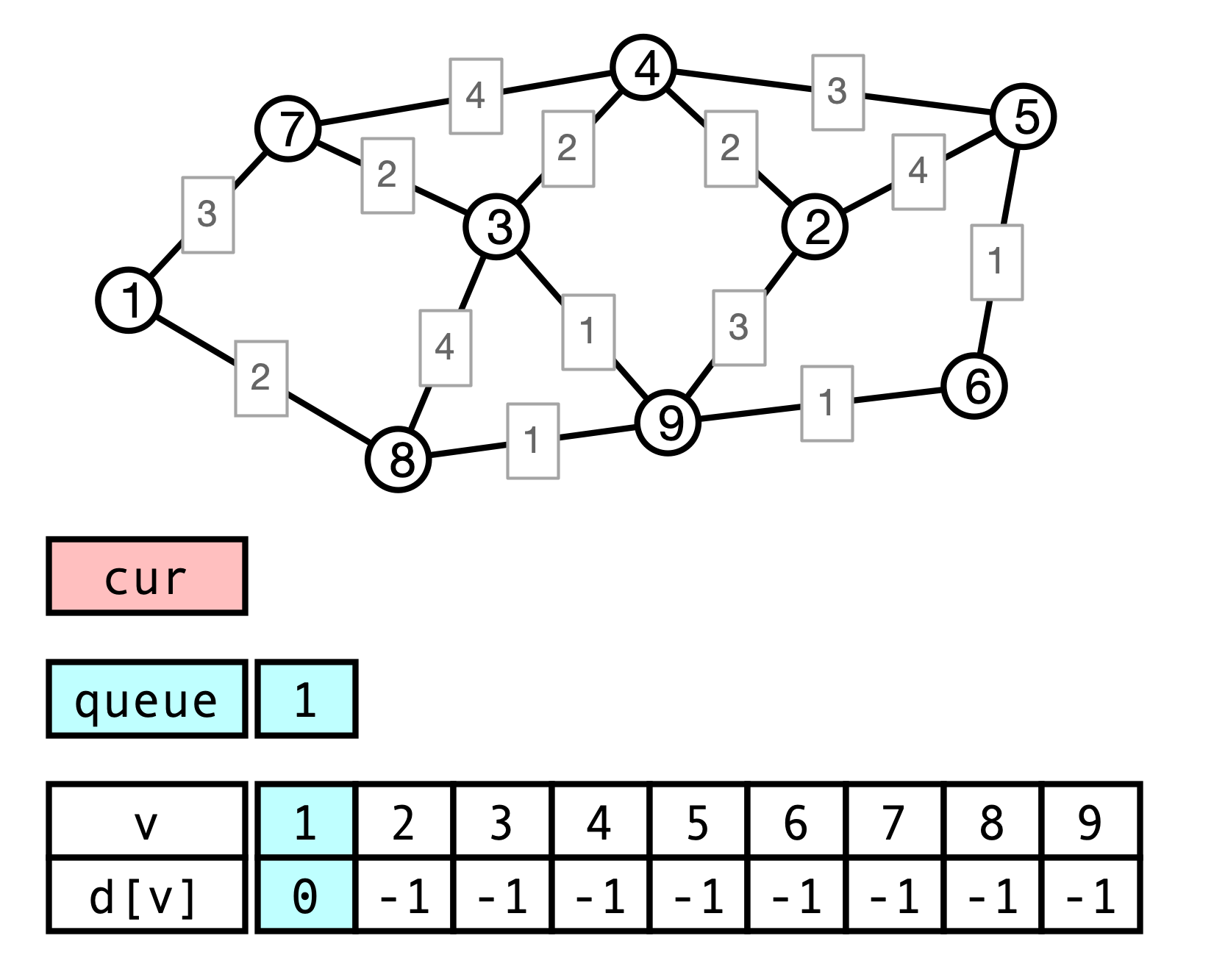
Issue
- BFS processes vertices in order of fewest hops from $u$
- With weighted graphs, shortest path need not have fewest hops
BFS Analysis Takeaway
-
BFS succeeds on unweighted graphs because closer vertices are processed before farther vertices
-
Could we get similar behavior for weighted distances?
-
must ensure: vertices processed in order of weighted distance from $u$
-
how can we do this?
-
- How could we efficiently implement a modified procedure?
Dijkstra’s Algorithm
Idea. Process elements in order of weighted distance from $u$
- Maintain set $S$ of nodes whose distances from $u$ is known
- Find element $x \in V - S$ that is closest to $u$ and add it to $S$
Dijkstra’s Algorithm in Detail
- Initialize $d[u] = 0$ and $d[v] = \infty$ for all $v \neq u$
- Maintain set $S$ of finalized nodes, initially empty
- Process nodes. While $S \neq V$ do:
- find node $v$ in $V - S$ with minimal $d[v]$
- add $v$ to $S$
- for each neighbor $x$ of $v$
- update $d[x] \gets \min (d[x], d[v] + w(v, x))$
Dijkstra Illustration
Correctness
- Initialize $d[u] \gets 0$ and $d[v] \gets \infty$ for all $v \neq u$
- Maintain set $S$ of finalized nodes, initially empty
- Process nodes: while $S \neq V$
- find node $v$ in $V - S$ with minimal $d[v]$
- add $v$ to $S$
- for each neighbor $x$ of $v$
- update $d[x] \gets \min (d[x], d[v] + w(v, x))$
Claim. For every vertex $v \in S$, $d[v]$ stores the correct (weighted) distance $d_w(u, v)$.
Proof of Claim
Claim. For every vertex $v \in S$, $d[v]$ stores the correct (weighted) distance $d_w(u, v)$.
Proof. Use induction on size of $S$. Set $k = $ size of $S$.
Base case $k = 1$. Only $u$ is added to $S$. Set $d[u] \gets 0$, which is correct answer.
Inductive Step I
Inductive hypothesis. When $S$ contains $k$ elements, $d[v]$ is correct for all vertices $v \in S$.
Consider next iteration of outer loop:
- $x$ has $d[x] = \min_{v \in S} (d[v] + w(v, x))$
Inductive Step II
Must show: $d[x] = d_w(u, x)$; argue by contradiction
- suppose $d[x] \neq d_w(u, x)$
- observe: there is a path from $u$ to $x$ of length $d[x]$
- $\implies d_w(u, x) < d[x]$
- $\implies$ there is a path $P$ from $u$ to $x$ of length $\ell < d[x]$
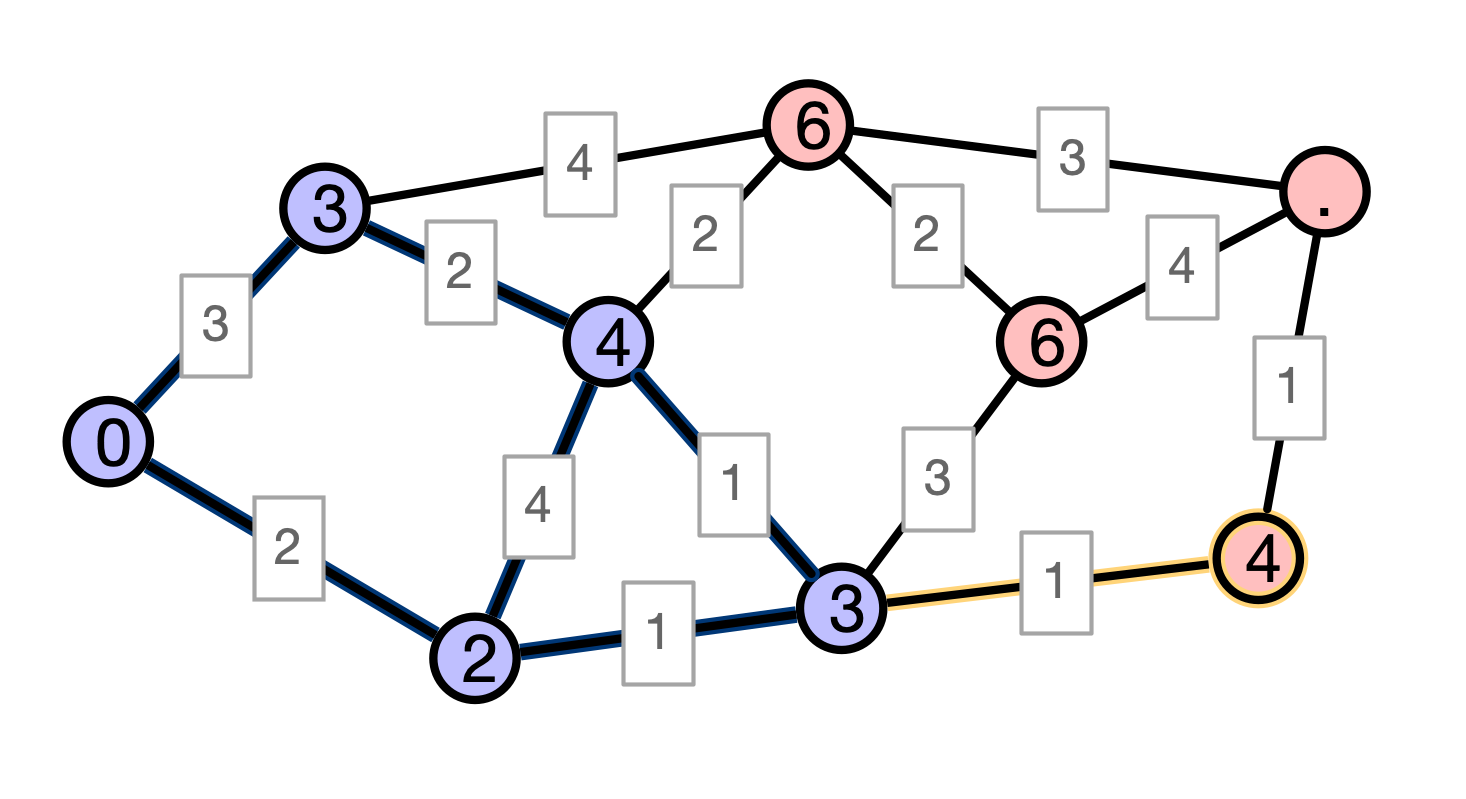
Shorter Path Illustration

Inductive Step III
Must show: $d[x] = d_w(u, x)$; argue by contradiction
- suppose $d[x] \neq d_w(u, x)$
- observe: there is a path from $u$ to $x$ of length $d[x]$
- $\implies d_w(u, x) < d[x]$
- $\implies$ there is a path $P$ from $u$ to $x$ of length $\ell < d[x]$
- $P$ must leave $S$ at some point $y$
- by definition of $x$, any path from $u$ to $y$ must be longer than $d[x]$
- $\implies w(P) \geq d[x]$, which contradicts $4$
Conclusion. $d[x] = d_w(u, x)$, as claimed.
Next Time
- Implementing Dijkstra’s algorithm
- how do we find $x$ with minimum $d[x]$ efficiently?
- review heaps/priority queues
- Minimum spanning tree problem